沪科版数学书八年级下册复习题C组第105页答案
1复习题C组第105页第1题答案
解:这个四边形是矩形
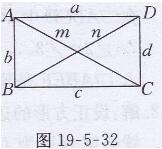
理由:如图19-5-32所示
四边形ABCD的边长分别为a,b,c,d,对角线为m,n
由题意得
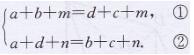
①+②,得a=c
代入①,得b=d
∴四边形ABCD是平行四边形
又∵a+b+m=a+d+n,
∴m=n
∴四边形ABCD是矩形
2复习题C组第105页第2题答案
证明:如图19-5-33所示,
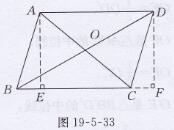
作AE⊥BC于点E,作DF⊥ BC,
交BC的延长线于点F
∵四边形ABCD为平行四边形,
∴ AB//=CD,
∴ ∠ABC=∠ DCF
又∵∠AEB=∠DFC=90°,
∴△ABE≌△DCF,
∴ BE=CF,AE=DF
∵在Rt△ABE中,AB2=AE2+BE2,
在Rt△ACE中,AC2=AE2+CE2,
在Rt△BDF中,BD2=DF2 +BF2,
∴AC2+BD2=AF2+CF2+DF2 +BF2
=2AE2 +(BC-BE) 2 +(BC+CF) 2
=2AE2 +(BC2 -2BC· BE-+BE2)+(BC2+2BC·CF+CF2)
=2AE2+ 2BC2+2BE2
=2AB2+2BC2
=2(AB2+BC2)
3复习题C组第105页第3题答案
解:如图19-5-34所示.设阴影部分的面积为x ,
它的左、右相邻两个(空白)三角形的面积为A,B,
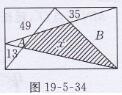
则A+x +B1/2S矩形
13+A+49+35+B=1/2S矩形
∴A+x+B=13+A+49+35+B
∴x=97
答:图中阴影部分的面积为97
4复习题C组第105页第4题答案
(1)证明:如图19-5-35所示,连接AC,BD,
交于点O,过点O作OO'⊥MN于点O'
∵AA'⊥MN,OO' ⊥MN, CC'⊥MN,
∴AA'//OO'//CC'
∵四边形ABCD是平行四边形,
∴OA=OC,
∴OO'是梯形AA'C'C的中位线,
∴OO'=1/2(AA'+CC')
同理OO'=1/2(BB'+DD'),
∴AA'+CC=BB'+DD'
(2)解:CC-AA' =BB'+DD'
证明:如图19-5-36所示,连接AC, BD交于O点,
连接AC.过点O作OO'⊥MN于点O',
(1)证明:如图19-5-35所示,连接AC,BD,
交于点O,过点0作OO'⊥MN于点O'
∵AA'⊥MN,OO' ⊥MN, CC'⊥MN,
∴AA'//OO'//CC'
∵四边形ABCD是平行四边形,
∴OA=OC,
∴OO'是梯形AA'C'C的中位线,
∴OO'=1/2(AA'+CC')
同理OO'=1/2(BB'+DD'),
∴AA'+CC=BB'+DD'
(2)解:CC-AA' =BB'+DD'
证明:如图19-5-36所示,连接AC, BD交于O点,
连接AC,过点O作OO'⊥MN于点O',
延长OO交AC'于E点

由(1)可知OO'是梯形BB'D'D的中位
线,∴OO'=号(BB'+DD')
∵OE是△ACC'的中位线,
∴OE=1/2CC'
∴O'E是△AA'C'的中位线,
∴O'E=1/2AA'
又∵OO' =OE-O'E ,
即1/2(BB'+DD')=1/2CC'-1/2AA' ,
∴CC'-AA'=BB'+DD'
(3)解 : AA'+DD'=BB'+CC'
证明:如图19-5-37所示,

连接AC,BD交于O点,连接AC',BD'
过O点作OO'⊥MN于O'点,
延长OO'交BD'于E点,交AC于F点,
可得OE是△BDD'的中位线
∴OE=1/2DD'
∵OF是△ACC'的中位线,
∴OF=1/2CC'
∵O'E是△BB'D'的中位线,
∴O'F=1/2BB'
∵O'F是△AA'C'的中位线,
∴O'F=1/2AA'
∵OO' =OF-O'F,CO'=OE-O'E,
∴OF-O'F=OE- O'E,
即1/2CC'=1/2AA'=1/2DD'=1/2BB'
∴CC '-AA' =DD'-BB'
∴AA'+DD'=BB'+CC
