人教版九年级下册数学南方新课堂28.2.3第6课时应用举例（3）答案

1课时达标第1题答案

13.4

2课时达标第2题答案

12

3课时达标第3题答案

30°

4课时达标第4题答案

利用坡度的意义

∵i=BC/AB=1/0.5

设BC=x，则AB=0.5x

在Rt△DCB中，tanD=BC/DB，即tan 30°=x/0.5+200

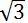∴x=0.5x+200，x=400（2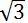+1）/11≈162

故山的高度约162米

5能力展示第1题答案

如下图所示：

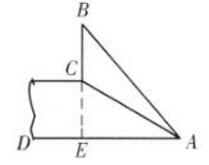
延长BC交AD于点E，则BC⊥AD

易知CE=5米，AE=5米

∴BE=11米

∴BC=6米

6能力展示第2题答案

(1)∵tan B=AF/BF=1/1.5

∴∠B≈34°

又∵tanC=DE/CE=1/3

∴∠C≈18°

答：坡角∠B约为34°,∠C约为18°

(2)在Rt△ABF中

∵i=AF/BF=6/BF=1/1.5

∴BF=9，AB=3≈10.8

在Rt△CDE中

∵i=DE/CE=6/CE=1/3

∴CE=18

∴AD=EF=BC-BF-EC=30-9-18=3

答：坝顶宽AD约为3m，斜坡AB的长约10.8m

7尝试提高第1题答案

(1)如下图所示：

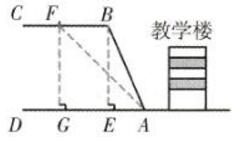
作BE⊥AD于点E

∵i=BE=AE=9/5

∴设BE=9x，AE=5x

在Rt△ABE中

∵BE²+AE²=AB²

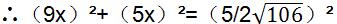
∴x=5/2

∴BE=9×5/2=45/2

答：改造前坡顶日到地面的垂直距离BE的长为45/2m

(2)连接AF，作FG⊥AD于点G

 当∠FAG= 45°时，FG=AG=BE=45/2

又∵AE=5x×5/2=25/2

∴BF=EG=AG-AE=45/2-25/2=10

答：BF至少是10 m

8尝试提高第2题答案

过点D，C分别作DE⊥AB，CF⊥AB于点E，F，如图所示：

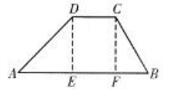
∵AD =8米，∠A =45

∴AE=DE=CF=4（米）

在Rt△CFB中，∠B=60°

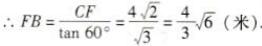
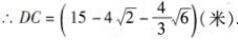
∴S梯形ABCD=1/2（15 +15 -4-4/3）×4≈60（米²）

∴60×2000 =120 000(米³)

答：这条坝共有12万米3