人教版九年级下册数学南方新课堂27.2.2第6课时相似三角形的性质
1课时达标第1题答案
1、(1) 13
(2) 100;5
2课时达标第2题答案
2、设两相似多边形的周长分别为C1cm和C2cm,面积分别为S1cm2和S2cm2.
根据题意得:
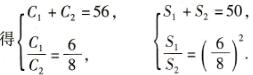
解得C1=24.C2=32,S1=18,S2=32
3课时达标第3题答案
3、(1)1:4:9
(2)1:3:5
4课时达标第4题答案
4、相等.可以证明AD/A'D'=EF/E'F'=BC/B'C'
5课时达标第5题答案
5、(1)∵DC=AC,CF平分∠ACB,
∴F为AD的中点.
又E为AB的中点.
∴EF∥BC
(2)由(1)得EF∥BC,
∴△AEF∽△ABD.
EF=1/2BD,
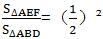

S△ABD=8
6能力展示第1题答案
1、∵四边形ABCD是平行四边形,∴AB∥CD.
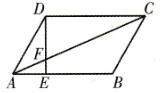
(第1题图)
∴∠ FAE=∠DCF, ∠FEA=∠FDC.
∴△AEF∽△CDF.
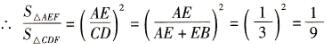
7能力展示第2题答案
2. OE//AD, OF//CD⇒∠BEO =∠BAD,
∠BOE=∠BDA ;
∠BOF=∠BDC,
∠BFO=∠BCD.
∴ △BOE ∽△BDA ; △BOF∽△BDC.
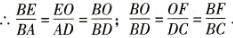
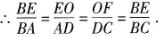
又∵∠EOF=∠ADC,
∴四边形EBFO∽四边形ABCD
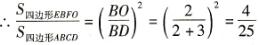
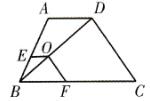
(第2题图)
8尝试提高第1题答案
1、(1)当△DEC的周长与四边形DABE的周长相等时,CD+ CE =AD+ BE +AB.
又∵CD+CE+ AD+ BE+AB=AB+BC+AC=12.
∴CD+CE=6
设CD =x,则CE =6 -x.
∵DE∥AB,
∴△CDE∽△CAB.
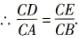
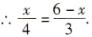
解得x=24/7,即DC=2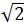
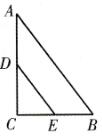
(第1题图)
(2)当△DEC的面积与四边形DABE的面积相等时,
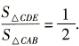
设CD=x
∵DE∥AB
∴△CDE∽△CAB.
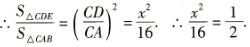
解得z=2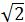 ,即DC=2
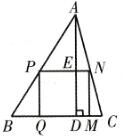
,即DC=2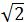 2、设正方形PQMN是符合要求的,△ABC的高AD与PN相交于点E,正方形PQMN的边长为x毫米.
2、设正方形PQMN是符合要求的,△ABC的高AD与PN相交于点E,正方形PQMN的边长为x毫米.
因为PN∥BC,
所以△APN∽△ABC.
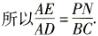
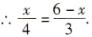 0
0
得x=48(毫米).
答:这个正方形零件的边长是48毫米
