青岛版数学书八年级下册第191页综合练习答案(3)
13第191页综合练习第13题答案
(本题答案不唯一,此处介绍一种)
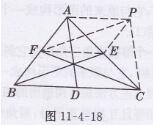
解:如图11- 4-18所示,过点F作FP//= BE,连接PC,AP,PE,EF,△PFC就是要求作的三角形
14第191页综合练习第14题答案
解:(1)BE=AD且BE⊥AD
(2)(1)中的结果仍然成立。
证明如下:∵∠ECB十∠BCD=∠BCD+ ∠DCA,
∴∠ECB=∠DCA
又∵EC=DC,BC=AC
∴AECB≌△DCA(SAS)
∴BE=AD,∠CEB= ∠CDA
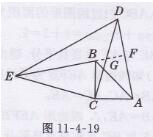
如图11-4-19所示,延长EB交AD于点F,交CD于点G,
在Rt△ECG中,
∵∠CEB+∠EGC=90°,
又∠EGC=∠DGF,
∴∠CDA-∠DGF= 90°,
∴∠DFG= 90°,
∴BE⊥AD
15第191页综合练习第15题答案
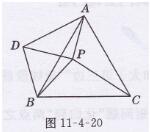
解:将△PBC绕点B逆时针旋转60°得△DBA,
如图11-4-20所示,
∵BD=BP,∠DBP=∠ABC=60°,
∴△BDP为等边三角形,∠DPB=60°
由旋转可知AD=PC=5 ,DP=BP=4,
∵AP2+DP2=32+42=52=AD2,
∴△ADP是直角三角形,∠APD=90°,
∴∠APB=∠APD+∠DPB=150°
16第191页综合练习第16题答案
解:(1)AF=CE
(2)AF=CE
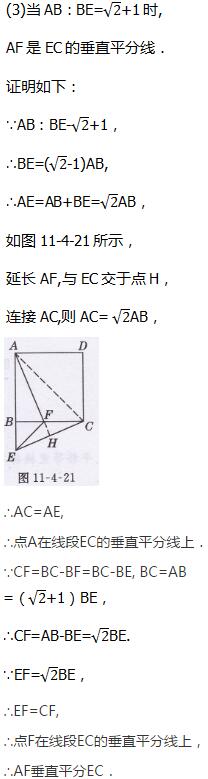
证明如下:∵∠ABF+∠FBC=90°,
∠CBE+∠FBC=90°,
∴∠ABF=∠CBH
又∵AB=CB,BF=BE,
∴△ABF≌△CBE(SAS),
∴AF=CE
17第191页综合练习第17题答案
解:(1)四边形ABFE是平行四边形,
证明如下:∵点A,C,F在同一条直线上,
AC= FC,点B,C,E在同一条直线上,BC=EC,
∴四边形ABFE是平行四边形
(2)当∠BAC=60°时,四边形ABFE是矩形
证明如下:∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形
∴△FEC是等边三角形,
∴AC=BC=CE=CF,
∴AC+CF=BC+CE,
即AF=BE,
由(1)知四边形ABFE是平行四边形,
∴四边形ABFE是矩形
改变∠BAC的度数,四边形ABFE不能成为菱形
