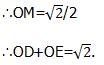青岛版数学书八年级下册第191页综合练习答案(2)

7第191页综合练习第7题答案

解：（1）四边形AECF是中心对称图形。理由如下：

∵四边形ABCD是平行四边形，

∴OA=OC，OB=OD

∵BE=DF,

∴OB+BE=OD+DF，即OE= OF

∴四边形AECF是平行四边形，

∴四边形AECF是中心对称图形

（2）对称中心是点O

8第191页综合练习第8题答案

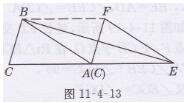
解：（1）连接BF，如图11- 4-13所示，由题意知△ABC∽ EFA，BA//EF，且BA=EF，

∴四边形AEFB为平行四边形，

∴S_□AEFB =2S_△ABC =2×3=6，

∴△ABC扫过的图形的面积为

S_□AEFB+S_△ABC=6+3=9

（2）BE与AF垂直且平分，理由如下：

由（1）知四边形AEFB为平行四边形，

∵AB=AC，AC=AE，

∴AB=AE，

∴四边形AEFB为菱形，

∴AF与BE互相垂直且平分

9第191页综合练习第9题答案

解：如图11-4-14所示，过点D作AC的平行线与BC的延长线相交于点E

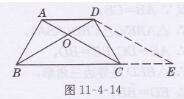
四边形ACED是平行四边形，即把AD平移到CE的位置，把AC平移到DE的位置，在△BDE中，BD= BD，AC= DE，BC+CE= BC+ AD，△BDE就是要求作的三角形

10第191页综合练习第10题答案

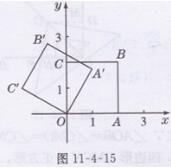
解：如图11- 4-15所示，正方形OA′B′C是正方形OABC旋转后的图形

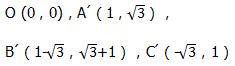
11第191页综合练习第11题答案

证明：如图11-4-16所示。过点B作BE//DC交AD于点E，

∴∠2=∠3

∵∠EBD+∠BDC=180° ,∠BDC=120° ,

∴∠EBD=60°

∵∠2+∠4=∠ABC=60°，

∠2+∠DBC=∠EBD=60°，

∴∠4=∠DBC

∵∠EBD=∠BAC= 60°，

∴∠2+∠DBC=∠1+∠DAC

又∵∠DBC=∠DAC

∴∠2=∠1，

∴∠1=∠3

又∵AB=CB

∴△ABE≌△CBD(ASA)，

∴AE=DC，BE=BD,

∴△BED是等边三角形，

∴ED=BD，

∴AE+ED=DC+BD，

即AD=BD+DC

12第191页综合练习第12题答案

证明：如图11-4 -17所示，过点C作CM⊥OA，

垂足为M，过点C作CN⊥OB，垂足为N

∵∠COM=45°,

∴∠OCM= 45°，

∴OM= CM

又∵∠AOB=∠CMO=∠CNO=90°,

∴四边形OMCN是正方形，

∴OM=ON

∵∠DCM=∠ECN,CM=CN，

∴△DCM≌△ECN(ASA)，

∴DM=EN

∴OD+OE=ON+EN+OD，

∴OD+OE=ON+DM+OD，

即OD+OE= 2OM

∵OM² +CM² =OC²