人教版九年级上册数学第二十一章综合练习配套练习册答案(2)

6第二十一章综合练习第三题第4题答案

（1）根据题意，关于x的方程x²-2（m+1）x+m²=0有两个实数根，

则方程的判别式⊿≥0 

⊿=[-2（m+1）] ²-4×1×m²=4m²+8m+4-4m²=8m+4，

所以8m+4≥0，8m≥-4，m≥ -（1/2） 

（2）根据题意，方程有两个不相等的实数根，则m>-（1/2），

假设m=1 把m=1代入方程x²-2（m+1）x+m²=0，

得x²-4x+1=0，

解得x₁=2+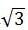，x₂=2-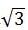

7第二十一章综合练习第三题第5题答案

解： 设可以排x人的方阵x²+6=（x-4）×2x-3，

解得x=9或x=-1（舍去），

人数为 9²+6=87人

8第二十一章综合练习第三题第6题答案

解：设定价为x元，每一台的利润为（x-2500）元，

依题意列方程得（x-2500）[8+ 2/100（3500-x）]=（3500-2500）×8×（1+12.5%）

整理得x²-6400x+10200000=0，

解得x₁=3000，x₂=3400； 

答：定价为3000或3400元时。

9第二十一章综合练习第三题第7题答案

（1）因为方程x²+（2k-3）x+k²=0有两个不相等的实数根， 

所以△＞0即（2k-3）2-4×1×k²＞0，

解得k＜3/4； 

（2）由根与系数的关系得：α+β=-（2k-3），αβ=k² 

因为α+β+αβ=6，

所以k²-2k+3-6=0，

解得k=3或k=-1， 

由（1）可知k=3不合题意，舍去

所以k=-1，

所以α+β=5，αβ=1， 

故（α-β）²+3αβ-5=（α+β）²-αβ-5=19