�˽̰���꼶�ϲ���ѧ��ҵ���ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2���𰸽���ʡ
ʱ��: 06-09
Ŀ¼
1�ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2����һ���
-3��5
2�ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2���ڶ����
y=-x2-2x+3
3�ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2���������
y=x2-2x-3
4�ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2���������
y=x2/8-x/4+2��y=-x2/8+3x*4+2
5�ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2���������
�⣺�߶��κ���y=-x2+bx+c�ĶԳ���Ϊx=2���Ҿ���ԭ�㣬
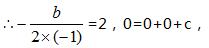
��b=4��c=0��
��y=-x2+4x
6�ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2���������
�⣺�������߽���ʽΪy=a��x+1��2-1������1��0�������

7�ڶ�ʮ����22.1.4���κ���y=ax2+bx+c��ͼ������ʣ�2���������
�⣺��������κ����Ľ���ʽΪy=ax2+bx+c��
�߶��κ�����ͼ����0��4������1��3������-1��4�����㣬

