苏科版九年级下册数学第5章课时9用二次函数解决问题（1）伴你学答案

1问题导学活动一答案

1、略

2、y=440×360+x（440-2x），能，求出二次函数的最大值即可

2问题导学活动二答案

1、略

2、填表略，设总产量为y kg，则有y=（10+x）（1000- 50x），解得x=5，

即当多投放鱼苗5千尾，可获得最大产量11250 kg

3问题导学活动三答案

1、AD=6 -1/4 πx-x；半径：1/2x；S=-（1/8π+1） x²+6x  

2、当x=24/（π+8）≈2.2，即当DC≈2.2，AD≈2.1时，窗户的透光面积最大

3、可以假设半圆的半径为x，过程略

4检测反馈第1题答案

a（1+x）²  

5检测反馈第2题答案

A

6检测反馈第3题答案

（1）y=-5x²+800x-27500（50≤x≤100）  

（2）当x=80时，y_最大值=4500    

（3）销售单价x满足82≤x≤90

7迁移运用第1题答案

（1）∵AD=EF=BC=x m，

∴AB=18 - 3x

∴水池的总容积为1.5x（18 - 3x）=36，

即x²-6x+8=0，解得x₁=2，x₂=4，

∴x应为2或4  

（2）由（1）可知，V与x的函数表达式为V=1.5x（18-3x）=-4.5x²+27x，且x的取值范围是0<x<6  

（3）V=-4.5x²+27x=-9/2（x-3）²+81/2

所以当x=3时，V有最大值81/2，即若使水池有总容积最大，x应为3，最大容积为40.5m³

8迁移运用第2题答案

（1）当1≤x<50时，y=（200- 2x）（x+40- 30）=-2x²+180x+ 2000；

当50≤x≤90时，y=（200-2x）（90-30）=-120x+12000

 

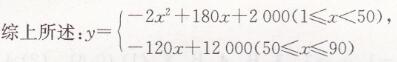
（2）当1≤x<50时，二次函数的图像开口向下；

当x=45时，y_最大值=6050；

当50≤x≤90时，y随x的增大而减小；

当x=50时，y_最大值=6000

综上所述，该商品在第45天时，当天销售利润最大，最大利润是6050元  

（3）当20≤x≤60时，即共有41天，每天销售利润不低于4800元