沪科版数学书九年级下册习题24.5答案
1习题24.5第1题答案
求证:(1)I与O重合;(2)ID=1/2OB
证明:(1)∵内心为I,∴I为角平分线的交点
∵外心为O,
∴O为各边垂直平分线的交点
又∵等边三角形顶角的平分线、底边上的高重合,
∴I与O重合.故等边三角形的内心、外心重合
(2)∵外接圆半径为OB即IB,内切圆半径为ID,
∴ID⊥BC
∴在Rt△IBD中,∠IBD=30°
∴ID=1/2IB=1/2OB
2习题24.5第2题答案
证明:连接IE、IF,
∵AB、AC与OI相切于点F、E,
∴IE⊥AC,IF⊥AB
∴∠AEI+∠AFI=180°
又∵在四边形AEIF中,
∠A+∠EIF+∠AFI+∠AEI=360°,
∴∠A+∠EIF=180°,
∴∠EIF=180°-∠A
∴∠FDE= 1/2∠EIF=1/2(180°-∠A)=90°-1/2∠A
3习题24.5第3题答案
解:连接OG、OE、OF
∵OO为△ABC的内切圆,切点为E、F、G,
由题意易知四边形OECF是正方形,
∴FC=EC=r
∴AF=AC-FC=4-r
∵AG=AF,
∴AG=4-r
∵AO平分∠BAC,
∴∠BAD=∠CAD
又∵∠AGO=∠C=90°,
∴△AGO≌△ACD
∴AG/GO=AC/CD,
即4-r/r,
∴r=4/5
4习题24.5第4题答案
证明:(1)如图24-5-36所示,△ABC的内切圆⊙I分别与AB、AC、BC切于点D、E、F,连接IE、IF
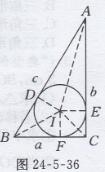
由题意,得四边形IECF是正方形,
∴EC=FC=r,
∴AE= b-r, BF=a-r
∵AE=AD,BF=BD,
∴AD=b-r, BD=a-r
又∵AB=AD+BD=b-r+a-r=c,
∴r=1/2(a+b-c)
(2)连接AI、BI、CI、DI
∵S△ABC=S△ABI+S△BCI+S△ACI=1/2c
R+1/2a•r+1/2b•r=1/2r(a+b+c),
又∵S△ABC=1/2ab,
∴1/2ab=1/2r(a+b+c),
∴r=ab/a+b+c
5习题24.5第5题答案
证明:由点E为内心, 得∠BAD=∠CAD
∴DB=DC,∴DB=DC
连接EC,则BCD=∠BAD=∠CAD, ∠BCE=∠ACE,
而∠DCE=∠DCB+∠BCE, ∠DEC=∠CAD+∠ACE,
∴∠DCE= ∠DEC,
∴DC=DE
∴DB=DC=DE
6习题24.5第6题答案
解:4个,三条直线围成一个三角形,它的三个内角平分线的交点为三角形的内心,它到三边的距离相等,三角形的外角平分线所在的三条直线两两相交,得三个交点,称为这个三角形的旁心,它们分别到三条已知直线的距离也是相等的,故符合条件的点共4个。
7习题24.5第7题答案
解:如图24-5-37所示,AB、BC、AC分别切⊙O于点F、D、E点,
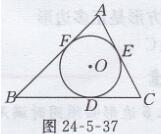
∴AF=AE,BF=BD, CD=CE
设AF=AE=x cm,BF=BD=y cm,CD=CE=z cm,

故AF=4 cm,BD=9 cm,CE=5 cm
