青岛版数学书八年级下册习题11.1答案(2)
6习题11.1第6题答案
解:∵点C(-1,3)与F(4,O)是一组对应点,
∴4-(-1)=5,0-3= -3
∴点F可以看作由点C向右平移5个单位长度,再向下平移3个单位长度得到的
∵A(-3,5),B(-2,1),
∴D(-3+5,5-3),E(-2+5,1-3)
即D(2,2),E(3,-2)
7习题11.1第7题答案
B′(-5,1),C'(-4,-5),D′(-1,- 6)
8习题11.1第8题答案
解:“柳叶”形的面积=1/4·π·42+12×4-1/4·π·42=4,
所以“柳叶”形的面积是4,
弧DG沿DE方向平移一个单位长度得到弧EB
9习题11.1第9题答案
解:(1)AC⊥CE.理由如下:
∵BD//CE,且BD⊥AC,∴AC⊥CE
(2)相等,理由如下:
因为这两个三角形等底、等高
(3)∵S△ACD=S△BEC,
∴S梯形ABCD=S△AEC
又∵ AC2CE,
∴S△AEC=1/2AC · CE
=1/2AC·BD=1/2ab,
∴S梯形ABCD=S△AEC=1/2ab
10习题11.1第10题答案
解:∵CD和EF的长为定值,
∴四边形CDEF的周长最小时,ED与CF之和最小
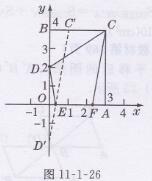
如图11-1-26所示,过点E作EC′//FC,与BC交于点C′,
由平移的性质,FC=EC
在y轴上作与点D关于x轴对称的点D′,
则ED= ED′,显然,要使ED与CF之和最小,
只需使ED′与EC′之和最小,当C′,E,D′三点在同一条直线上时,
ED′与EC′之和最小,
∵C(1,4),D′(0,- 2)
设直线CD′的表达式为y=kx+b(k≠0),

∴直线CD′的表达式为y =6x-2
∵点E在直线C′D′上,且纵坐标为0,
∴x=1/3
∴点E的坐标为(1/3,0),
点F的坐标为(7/3,0)
