青岛版数学书八年级下册习题6.4答案
1习题6.4第1题答案
解:(1)矩形。
已知:如图6-4-21所示,在四边形ABCD中,对角线AC⊥BD,点E,F,G,H 分别为AB,BC,CD,DA的中点。
求证:四边形EFGH是矩形
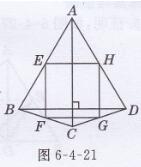
证明:∵点E,F是AB,BC的中点,
∴EF//AC
同理,FG//BD,GH//AC,EH//BD,
∴四边形EFGH是平行四边形
又∵ACIBD,
∴EF⊥FG
∴□EFGH是矩形
(2)平行四边形。
已知:如图6-4-22所示。在□ABCD中,点E,F,G,H分别为AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形
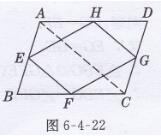
证明:连接AC
∵点E,F分别是AB,BC的中点,
∴EF//AC且EF=1/2AC
同理,GH//AC且GH=1/2AC
∴EF//HG且EF=HG
∴四边形EFGH是平行四边形
(3)正方形。
已知:四边形ABCD是正方形,点E,F,G,H分别是AB,BC,CD,DA的中点
求证:四边形EFGH是正方形。
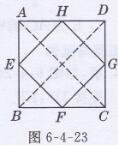
证明:如图6-4-23所示,连接AC,BD。
∵E,F分别是AB,BC的中点,
∴EF//AC且EF=1/2AC
同理,GH∥AC且GH=1/2AC,EH∥BD 且EH=1/2BD,FG//BD且FG=1/2BD
∵在正方形ABCD中,
AC=BD且AC⊥BD,
∴ EF⊥EH且EF=FG=GH-EH
∴四边形EFGH是正方形
2习题6.4第2题答案
已知:如图6-4- 24所示,点D,E,F分别为△ABC中AB,BC,AC的中点
求证:AE,DF互相平分
证明:如图6-4-24所示,连接DE,EF

∴D,E分别为AB,BC的中点,
∴DE//AC
同理,EF//AB
∴四边形ADEF是平行四边形
∴AE,DF互相平分
3习题6.4第3题答案
证明:如图6-4-25所示,取BC的中点F,连接DF
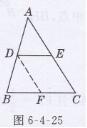
∵D是AB的中点,
∴DF//AC
又∵DE∥BC,
∴四边形DECF为平行四边形,
∴DF= EC
又∵DF是△ABC的中位线,
∴DF=1/2AC,
∴EC=1/2AC
∴E为AC的中点
∴AE= EC
4习题6.4第4题答案
解:如图6-4-26所示,取BC的中点F,连接DF,EF
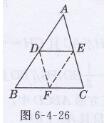
又∵D,E是AB,AC的中点,
∴DE//BC,EF//AB
∴四边形DBFE是平行四边形
∴S△DEF=S△DBF
同理,S△DEF=S△EFC,S△DEF=S△ADE
∴S△ADE=S△ABD=S△DEF=S△EFC
∴S△ADE/S△ABC=1/4
5习题6.4第5题答案
解:∵D1,D2,D3是BC的四等分点,
E1,E2,E3是AC的四等分点,
F1,F2,F3是AB的四等分点,
∵△ABC的面积为1,
∴阴影三角形Pl,P3,P4的面积分别为△ABC面积的1/16,
阴影三角形P2是指△D2 E2 F2
所以阴影三角形P2的面积为△ABC面积的4/16=1/4
∴四个阴影三角形Pl,P2,P3,P4的面积之和为
1/16+1/4+1/16+1/16=7/16
6习题6.4第6题答案
明:如图6-4-27所示,连接EG

∵AD⊥BC,
∴∠ADB=90°,
在Rt△ABD中,
∵E是AB的中点,
∴DE=1/2AB
∵G,F分别是△ABC的边AC,BC的中点,
∴GF=1/2AB
∴DE= GF
同理,DG=EF
又∵EG=GE,
∴△EDG≌△GFE( SSS),
∴∠EDG= ∠GFE
