青岛版数学书八年级下册习题6.1答案
1习题6.1第1题答案
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D
∵∠A:∠B=7:2,
∴设∠A=7x°,则∠B=2x°
又∵在□ABCD中,AD∥BC,
∴∠A+∠B=180°
∴7x+2x=180
∴x= 20
∴∠A= 140o,∠B= 40°
∴∠C=140°, ∠D=40°
2习题6.1第2题答案
解:如图6-1-32所示,过A,D分别作AE⊥BC, DF⊥BC,垂足分别为E,F,
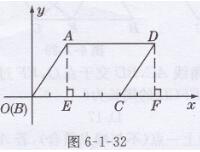
∴∠AEB= ∠DFC=90°
∵在□ABCD中,AD∥BC,
∴AE=DF
又∵在□ABCD中,AB=DC
∴ Rt△ABE≌Rt△DCF( HL)
∴OE= CF=2,DF=AE=3
∵AD=EF=OC=5,
∴OF=OE+EF= 2+5=7,
∴D点坐标为(7,3)
3习题6.1第3题答案
解:图中相等的线段有:AB=DE, BC=EF,AC=DF,AD=BE=CF
证明:∵∠1∥∠2,∠3 //∠4
∴四边形ABED是平行四边形(定义)
∴AB=DE,AD=BE
同理,BC=EF, BE=CF,AC= DF,AD=CF
∴AD=BE=CF
4习题6.1第4题答案
解:图中共有4对三角形全等,
即△AOB≌△COD,
△AOD≌△COB,
△ABD≌△CDB,
△ABC≌△CDA
证明:∵四边形ABCD是平行四边形,
∴AD=CB,AB=CD
又∵BD=DB
∴△ABD≌△CDB(SSS)
同理,△ABC≌△CDA
∵四边形ABCD是平行四边形,
∴ AD=CB, OA=OC, OD=OB
∴△AOD≌△COB(SSS)
同理,△AOB≌△COD
5习题6.1第5题答案
解:相等,
证明:如图6-1-33所示,过点0作OE⊥AD,OF⊥BC,垂足分别为E,F
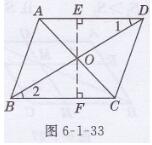
∵四边形ABCD是平行四边形,
∴AD//BC,OB=OD
∴∠1=∠2
又∵OE⊥AD, OF⊥BC,
∴∠DEO=∠BFO= 90°
∴ADOEccn△BOF(AAS)
∴OE=OF
即点O到AD,BC的距离相等
同理,点O到AB与CD的距离相等
6习题6.1第6题答案
解:∵AE平分∠BAD,
∴∠BAE=∠DAE
∵四边形ABCD是平行四边形
∴AB∥CD,CD=AB=10 ,AD=BC=6
∴∠BAE=∠AED
∴∠AED=∠DAE
∴DE=AD=6
∴CE=CD-DE=10-6=4
7习题6.1第7题答案
解:∵四边形ABCD是平行四边形,
∴OB=OD
又∵OE⊥BD
∴EB=ED
∴△ABE的周长=AB+AE+EB-AB+AD
∵在□ABCD中,AB=DC,AD=BC,
∴□ABCD的周长=2(AD+AB)
∴△ABE的周长:□ABCD的周长=1:2
8习题6.1第8题答案
解:(1) S1=S2=S3=S4
如图6-1-34所示,

过点A,C分别作AE⊥BD,CF⊥BD,
垂足分别为E,F,
故∠AEO=∠CFO= 90°,
∵四边形ABCD是平行四边形,
∴OA=OC
又∵∠AOB=∠COD
∴△AOE≌△COF(AAS)
∴AE=CF
又∵S1 =1/2OB•AE,
S2=1/2OB•CF,
S3=1/2OD•CF,
S4=1/2OD•AE,
∴S1=S2=S3=S4
(2)S1:S2 =S4:S3
如图6-1-35所示,
在四边形ABCD中,AC⊥BD
∴S1=1/2AO•BO,
S2=1/2OC•BO,
S3 =1/2OC•DO,
S4 = 1/2AO•DO
∴S1:S2 =AO:OC,
S4:S3 =AO:OC
∴Sl:S2 =S4:S3
(3)S1•S3 =S2•S4
或表示为S1:S2=S4:S3 ,
S1:S4 =S2:S3
如图6-1-36所示,
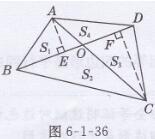
过点A、C分别作AE⊥BD、CF⊥BD,垂足分别为E,F
故S1= 1/2BO•AE
S2 =1/2BO•CF,
S3=1/2OD•CF,
S4 =1/2OD•AE,
∴S1•S3 =1/2BO•AE×1/20D•CF=1/4AE•CF•BO•OD,
S2•S4 =1/2BO•CF×1/2OD•AE=1/4AE•CF•BO•OD
∴S1•S3 =S2•S4
或者表示为S1:S2 =AE:CF, S4:S3 =AE:CF,
即S1:S2 =S4:S3
同理:S1:S4 =S2:S3
