冀教版九年级上册数学第二十四章24.3一元二次方程根与系数的关系轻轻松松学数学答案(2)

6一元二次……关系第9题答案

解：设方程的两个实数根为x₁，x₂，

则x₁+x₂=2（m-2），x₁•x₂=m² 

令x₁²+ x₂²=56，得

（x₁+x₂）²- 2 x₁x₂=4（m-2）² -2m² =56， 

解这个方程得，m-10或m=-2

当m=10时，△<0，所以不合题意，应舍去， 

当m=-2时，△>0，符合题意， 

所以存在实数m=-2，使得方程的两个实数根的平方和等于56

7一元二次……关系第10题答案

解：设边AB=a，AC=b， 

∵a，b是方程x²-（2k+3）x+k²+3k+2=0的两根， 

∴a+b=2k+3，a•b=k²+3k+2 

又∵△ABC是以BC为斜边的直角三角形，且BC=5， 

∴a² +b²=5²，即（a+b）²-2ab=5²， 

∴（2k+3）²-2（k²+3k+2） =25， 

∴k²+3k-10=0， 

∴k₁=-5或k₂=2 

当k=-5时，方程为x²+7x+12=0，解得x₁=-3，x₂=-4（舍去）； 

当k=2时，方程为x²-7x+12=0，解得x₁=3，x₂=4

∴当k=2时，△ABC是以BC为斜边的直角三角形

8一元二次……关系第11题答案

解：（1）∵方程有实数解， 

∴b²-4ac=2² -4（k+1）≥0，解得k≤0 

∴k的取值范围是k≤0 

（2）根据一元二次方程根与系数的关系得

x₁+x₂=-2，x₁x₂=k+1 

∴x₁+x₂- x₁x₂=-2-（k+1） 

由已知，得2-k-1<-1，解得k> -2

又由（1）得k≤0，∴-2<k≤0

∵k为整数， 

∴k的值为-1或0

9一元二次……关系第12题答案

解：∵关于x的一元二次方程4x² +4（m-1）x+m² =0有两个非零实数根， 

∴b² -4ac=[4（m-1）]² -4×4m²= -32m+16≥0， 

∴m≤1/2

又x₁，x₂是方程4x²+4（m-1）x+m² =0的两个实数根， 

∴由一元二次方程根与系数的关系，得：

x₁+x₂=-（m-1），x₁•x₂=（1/4）m² 

假设x₁，x₂同号，则有两种可能： 

（1）x₁<0，x₂<0；

（2）x₁>0，x₂>0

若x₁<0 ，x₂<0 

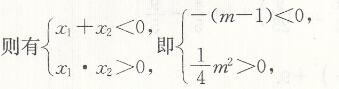
解这个不等式组得m>1

∵m≤1/2时方程才有实数根， 

∴此种情况不成立 

若x₁>0，x₂>0，

 

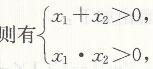
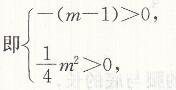
解这个不等式组，得m<1 

又∵m≤1/2，

∴当m≤1/2时，两根能同号