北师大版九年级下册数学书习题3.10答案
1习题3.10第1题答案
解:如下图所示:
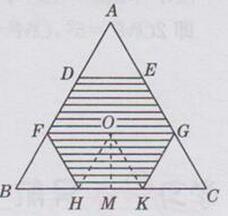
设正六边形的中心为点O,连接OH,OK,过点O作OM⊥HK.垂足为M.
由题意知:△ADE≌△BHF≌△CKG,且△ADE,△BHF,△CKG均为等边三角形
设其边长为x(x>0),则知3x=6
∴x=2,即正六边形DFHKGE的边长为2
可将正六边形DF HKGE分成6个边长为2的正三角形
在等边△HOK中,∠HOK =60°,OH=2,HM=1/2HK=1,∠HOM=1/2∠HOK=1/2×60°=30°
∴OM=OH·cos 30°=2×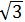 /2=
/2=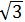
∴S正六边形DEHKGE=6S△OHK =6×1/2HK·OM=6×1/2×2×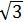 =6
=6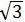
2习题3.10第2题答案
解:如下图所示:
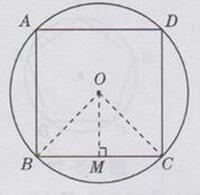
连接OB,OC,过点O作OM⊥BC,垂足为M
在△BOC中,OB=OC,∠BOC=1/4×360°=90°
∴∠MOC= 1/2∠BOC= 1/2×90°=45°
∴∠OCM= 90°-∠MOC=90°- 45°=45°
∴∠MOC=∠OCM
∴OM=MC
又∵在Rt△OMC中,由勾股定理得:
OM2+MC2=OC2,即20M2=62 ,OM2 =18,
∴OM=3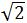 cm,MC=OM=3
cm,MC=OM=3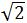 cm
cm
由垂径定理知MC=1/2BC
∴BC=2MC=6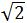 cm
cm
∴S△OBC=1/2BC·OM
=1/2 ×6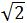 ×3
×3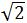 =18(cm2)
=18(cm2)
∴S正方形ABCD=4S△OBC=4X18=72(cm2)
∴圆内接正四边形的边长为6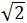 cm,边心距为3
cm,边心距为3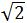 cm,面积为72cm2
cm,面积为72cm2
3习题3.10第3题答案
(1)各边相等的圆内接四边形一定是正方形,根据各边相等可得各边所对的劣弧也相等,各边所对的圆心角都相等,且都等于(360°)/4=90°,两条相邻边所对圆心角之和为180°,所以四边形的两条对角线都是经过圆心的线段,即是圆的直径,根据直径所对的圆周角是90°,可得四边形的四个内角都为直角,所以这个四边形既是菱形又是矩形,故一定是正方形
(2)各角相等的圆内接四边形不一定是正方形,例如:矩形
4习题3.10第4题答案
(1)如下图所示:
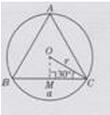
过点O作OM⊥BC于点M,△ABC为圆内接正三角形
∠OCM=1/2∠ ACB=1/2×60°=30°,OM= 1/2OC=1/2r,CM2=OC2-OM2=r2-(1/2 r)2=3/4r2
∴CM=/2r.
∴a=BC=2CM=r
如下图所示:
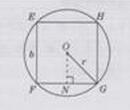
过点O作ON⊥FG于点N,则∠NOG=∠NGO=45°
由勾股定理得:ON=GN=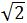 /2r
/2r
∴b=FG=2GN=2×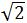 /2r=
/2r=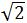 r
r
如下图所示:
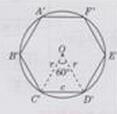
对于正六边形A'B'C'D'E'F',OC'=OD'=C'D'=r=c
综上所述,a=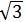 r,b=
r,b=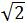 r,c=r
r,c=r
(2)∵a=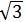 r,b=
r,b=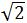 r,c=r
r,c=r
∴c2 =r2,b2 =2r2,a2 =3r2
∴c2 +b2 =3r2 ,a2 =b2 +c2
∴a,b,c为三边能构成三角形,且是以b,c为直角边,a为斜边的直角三角形
5习题3.10第5题答案
解:如下图阴影部分所示:
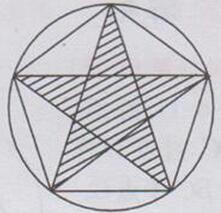
得到一个正五角星(注:此题答案不唯一,合理即可)
