华东师大版数学书八年级下册习题18.2答案
1习题18.2第1题答案
解:当两个全等三角形是锐角三角形时,可以拼成6个四边形;当两个全等三角形是直角三角形或钝角三角形时,可以拼成4个四边形,但是两个全等三角形拼成的4个四边形,但是两个全等三角形拼成的四边形中,只有3个是平行四边形,因为对边分别相等的四边形是平行四边形。
2习题18.2第2题答案
证明:如图18-2-36所示,
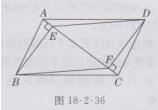
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴∠BAC=∠ACD,
∵BE⊥AC,DF⊥AC
∴BE//DF,∠AEB=∠CFD=90°,
∴△ABE ≌ △CDF,
∴BE=DF,
∴四边形BEDF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
3习题18.2第3题答案
证明:如图18-2-37所示。
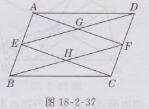
∵四边形ABCD是平行四边形,
∴AB=//CD,AB=CD,
∵E,F分别是AB,CD的中点,
∴AE=BE=CF=DF,
∴AE∥=CF,BF∥=DF,
∴四边形BFDF与四边形AECF都是平行四边形。
∴BF∥DE,AF∥CE,即EG∥FH,EH∥FG,
∴四边形EHFG是平行四边形
(两组对边分别平行的四边形是平行四边形)
4习题18.2第4题答案
证明:如图18-2-38所示
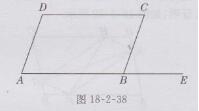
∵∠C=∠CBE,
∴AB∥DC,
∵AB=DC,
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
∴AD=BC
5习题18.2第5题答案
证明:如图18-2-39所示,连接DM。
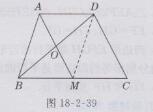
∵AM,BD互相平分,
∴四边形ABMD是平行四边形,
∴AD∥BM,AD=BM,
∵M是BC的中点,
∴BM=CM,
∴AD=CM,
又∵AD∥CM,
∴四边形AMCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
∴AM∥=DC
