冀教版九年级上册数学第二十四章24.4一元二次方程的应用轻轻松松学数学答案(2)

7一元二次方程的应用第10题答案

解：设每件商品售价为x元，才能使商店赚400元，

根据题设，得（x-21）（350-10x） =400

解得x₁=25，x₂=31 

又因为21×（1+20%）=25.2，

而x₁<25.2，x₂>25.2，

所以x₂=31应舍去

当x=25时，350-10x=350-10×25=100（件）

答：该商店要卖出100件商品，每件售价为25元。

8一元二次方程的应用第11题答案

解：设原来的两位数的十位数字为x，则个位数字为5-x，

根据题意得[10x+（5-x）][10（5-x）+x]=736，

解得x₁=2，x₂=3 

当x=2时，5-x=3待合题意，则原来的两位数是23

当x=3时，5-x=2符合题意，则原来的两位数是32

答：原来的两位数是23或32

9一元二次方程的应用第12题答案

解：（1）设每千克核桃应降价x元 

根据题意，得（60- x-40）（100+x/2 ×20）=2240

化简，得，x²-10x+24=0，

解得x₁=4，x₂=6 

答：每千克核桃应降价4元或6元 

（2）由（1）可知每千克核桃可降价4元或6元

因为要尽可能让利于顾客，所以每千克核桃应降价6元

此时，售价为60-6=54（元），54/60×100%=90%

答：该店应按原售价的九折出售。

10一元二次方程的应用第13题答案

解：（1）26.8

（2）设需要售出x部汽车，

由题意可知，每部汽车的销售利润为

28-[27-0.1（x-1）]=0.1x+0.9（万元）

当0≤x≤10时，

根据题意，得x•（0.1x+0.9）+0.5x=12

整理，得x²+14x-120=0

解这个方程，得x₁=-20（不合题意，舍去），x₂=6 

当x>10时，

根据题意，得x•（0.1x+0.9）+x=12. 

整理，得x²+19x-120=0

解这个方程，得x₃=-24（不合题意，舍去），x₄=5

因为5<10，所以x=5（舍去）

答：需要售出6部汽车。

11一元二次方程的应用第14题答案

解：（1）设2012年甲校响应本校倡议的人数为x，乙校响应本校倡议的人数为（60-x）

依题意，得18x+6（60-x）=600，

解得x=20，60- x=40 

∴2012年两校响应本校倡议的人数分别是20和40 

（2）设2012年到2014年，甲校响应本校倡议的人数每年增加 m；乙校响应本校倡议的人数每年增长的百分率为 n

依题意，得 

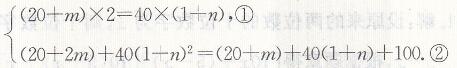
由①得m=20n，代入②并整理得2n² +3n-5=0， 

解得n=1，n=-2.5（负值舍去）， 

∴m= 20， 

∴2014年两校响应本校倡议减排二氧化碳的总量为：

（20+2×20）×18+40（1+1）²×6=2040（kg）， 

答：2014年两校响应本校倡议减排二氧化碳的总量为2040 kg