浙教版九年级上册数学第1章复习题课时特训答案(2)

8第1章复习题第17题答案

y=- 1/8x²- 1/4x+1

9第1章复习题第18题答案

（1）S=-2x²+32x     

（2）x=8，S最大=128

10第1章复习题第19题答案

（1）设抛物线的解析式为y=ax²+c 

∵B（140，0），E（70，42），

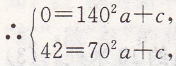
∴a=-1/350，c=56，

∴y=（-1/350）x²+56=56

（2）当x=0时，y=（-1/350）x²+56=56

∴OC=56米 

设存在一根系杆的长度是OC的一半，即这根系杆的长度是28米， 

则28=（-1/350）x²+56，得

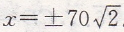
∵相邻系杆之间的间距均为5米，最中间系杆OC在y轴上， 

∴每根系杆上的点的横坐标均为整数 

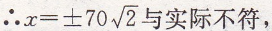
∴不存在一根系杆的长度恰好是OC长度的一半

11第1章复习题第20题答案

（1）y=-10x²+100x+6000 

（2）单价定为85元时，每月销售该商品的利润最大，最大利润为6250元

12第1章复习题第21题答案

（1）将M（-2，-2）代入抛物线的解析式得

-2=1/a（-2-2）（-2+a）

解得a=4 

（2）①由（1）抛物线解析式y=1/4（x-2）（x+4）

当y=0时，得0=1/4（x-2）（x+4）

解得x₁=2，x₂=-4 

∵点B在点C的左侧， 

∴B（-4，0），C（2，0） 

当x=0时，得y=-2，即E（0，-2）， 

∴S三角形BCE=1/2 ×6×2=6；

②由抛物线的解析式y=1/4（x-2）（x+4），

得对称轴为直线x=-1， 

根据C与B关于抛物线的对称轴直线x=-1对称， 

连接BE，与对称轴交于点H，即为所求， 

设直线BE的解析式为y=kx+b，

将B（-4，0）与E（0，-2）分别代入得

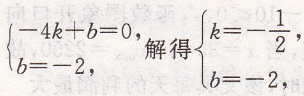
∴直线BE的解析式为y=-（1/2）x-2， 

将x=-1代入得y=1/2-2=-3/2，

则H（-1，-3/2）

13第1章复习题第22题答案

（1）该商场销售彩电的总收益为800×200=160000（元） 

（2）依题意可设y=k₁x+800，z=k₂x+200 

∴400k₁+800=1200，200k₂+200=160，

解得k₁=1，k₂=-1/5 

∴y=x+800，z=（-1/5）x+200

（3）w=yz=（x+800）[（-1/5）x+200）]=-1/5（x-100）²+162000

∴政府应将每台补贴款额x定为100元，

总收益有最大值，其最大值为162000元