浙教版九年级上册数学第1章1.4二次函数的应用（二）课时特训答案(2)

7二次函数的应用（二）第7题答案

4

8二次函数的应用（二）第8题答案

4

9二次函数的应用（二）第9题答案

3

10二次函数的应用（二）第10题答案

（1）由题意得，销售量=250-10•（x-25）=-10x+500 

则ώ=（x-20）（-10x+500）=-10x²+700x-10000 

（2）ώ=-10x²+700x-10000=-10（x-35）²+2250 

∵-10<0 

∴函数图象开口向下，ώ有最大值，

当x=35时，ώmax=2250， 

故当单价为35元时，该文具每天的利润最大 

（3）A方案的利润高，理由如下：

A方案中：20＜x≤30，

故当x=30时，ώ有最大值，此时ώA=2000；

B方案中：

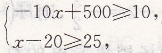
故x的取值范围为：45≤x≤49

∵函数ώ=-10×（x-35）²+2250，对称轴为x=35

∴当x=45时，ώ有最大值，此时ώB=1250，

∵ώA＞ώB

∴A方案的利润最高

11二次函数的应用（二）第11题答案

（1）y₁=2x（x>0），y₂=（1/2）x²（x>0） 

（2）14万元 ；32万元

12二次函数的应用（二）第12题答案

（1）∵AB=8.由抛物线的对称性可知OB=4 

∴B（4，0），0=16a-4  

∴a=1/4 

（2）过点C作CE⊥AB于E，过点D作DF⊥AB于F

∵a=1/4   

∴y=（1/4）x²-4   

令x=-1 

∴m=1/4×（-1）²-4=- 15/4 

∴C（-1，-15/4），

∵点C关于原点的对称点为点D，

∴D（1,15/4）

∴CE=DF=15/4

∴S∆BCD=S∆BOD+S∆BOC=1/2 OB·DF+1/2 OB·CE

=1/2 ×4× 15/4+1/2 ×4 ×15/4=15（平方米）

∴∆BCD的面积为15平方米